MODULES

Natural Convection In 2-D Differentially Heated Cavity

Problem Definition:

The problem consists of a cavity having dimensions 1X1 with higher temperature on the left side (Th=1) and lower temperature on the right side (Tc=0). The other two walls are considered to be adiabatic. The velocities at all solid walls are considered to be equal to 0 and gravity is assumed to be present in the flow. Figure 5.2 shows the computational geometry showing mesh structure and size (approx. 6000). The mesh consists of both quadrilateral and triangular cells.


Figure 5.1

Results:

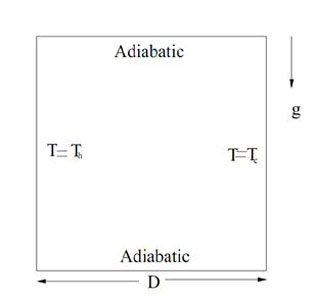
Numerical simulations have been carried for different Rayleigh numbers. The streamlines and isotherms are plotted for Rayleigh numbers equal to 103, 104, 105 as shown in Figs. 5.2-5.3. The comparison of maximum Nusselt number (at the hot wall) for different Rayleigh numbers are also shown in Table 5.1.

(a)


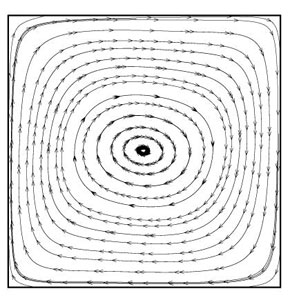
(b)


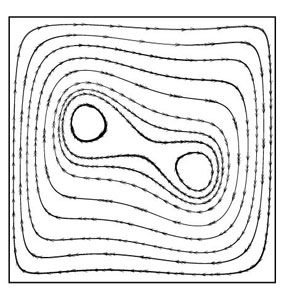
(c)
Figure 5.2: Streamlines for (a) Ra=103 (b) Ra=104 (c) Ra=105


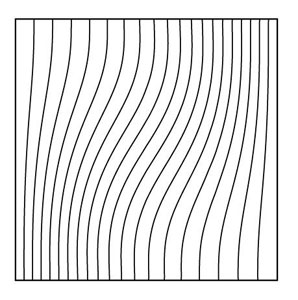
(a)


(b)


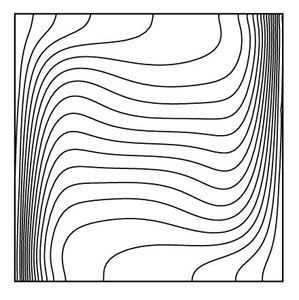
(c)
Figure 5.3: Isotherms for (a) Ra=103 (b) Ra=104 (c) Ra=105

Table 5.1: Comparison of maximum Nusselt Number (at the hot wall)



a) De Vahl Davis G. , ‘Natural Convection of Air in a Square Cavity: a Benchmark Numerical Solution’ , International Journal of Numerical Methods in Fluids, Vol. 3 , pp. 249-264,1983.

b)Markatos N.C. and Perikleous K.A., ‘Laminar and Turbulent Natural Convection in an Enclosed Cavity’ , International Journal of Heat and Mass Transfer ,Vol. 27 ,pp. 755-772,1984

c)Hadijisophocleous G.V., Sousa A.C.M, Venart J., ‘Prediction of Transient Natural Convection in Enclosures of Arbitrary Geometry Using a Non-Orthogonal Numerical Model’, Numerical Heat Transfer, Vol.13 ,pp.373-392,1988.

d) Present Study

e)% error = d-a/d *100%